Introduction
When it comes to solving challenging Primary 5 Math word problem sums, applying the right strategy can make all the difference!
For the topic of Whole Numbers, one effective problem-solving approach is to use Change Strategies. The four sub-types of Change Strategies are:
1️⃣ One Item Unchanged
2️⃣ Total Unchanged
3️⃣ Difference Unchanged
4️⃣ Everything Changed
These strategies guide your child to spot what has changed and what has stayed the same, helping them to solve problems more clearly and accurately.
In this blog post, we’ll focus on the first Change Strategy: One Item Unchanged, also known as One Item the Same.
I will show you how to apply this strategy step by step, using a model to visualise the problem and work towards the solution.
You can also watch my explainer video for free by visiting our YouTube channel.
Let’s Take A Look At This Whole Numbers Question

Source: CHIJ St. Nicholas Girls’ School (Primary) – 2010 P5 CA1 Examination Paper
Read Also:
Step 1: Understand the Problem Using ACE Strategy
💡 What Is The ACE Strategy? 💡
A – At First
C – Change
E – End
We’ll use a model at each stage to track how Tanisha’s and her sister’s money changes.
Step 2: Identify Key Information
Should we begin by drawing the At First model or the End model?
You should decide based on the keywords in the question.
Here is the order of key phrases to look for when deciding which model to start with:
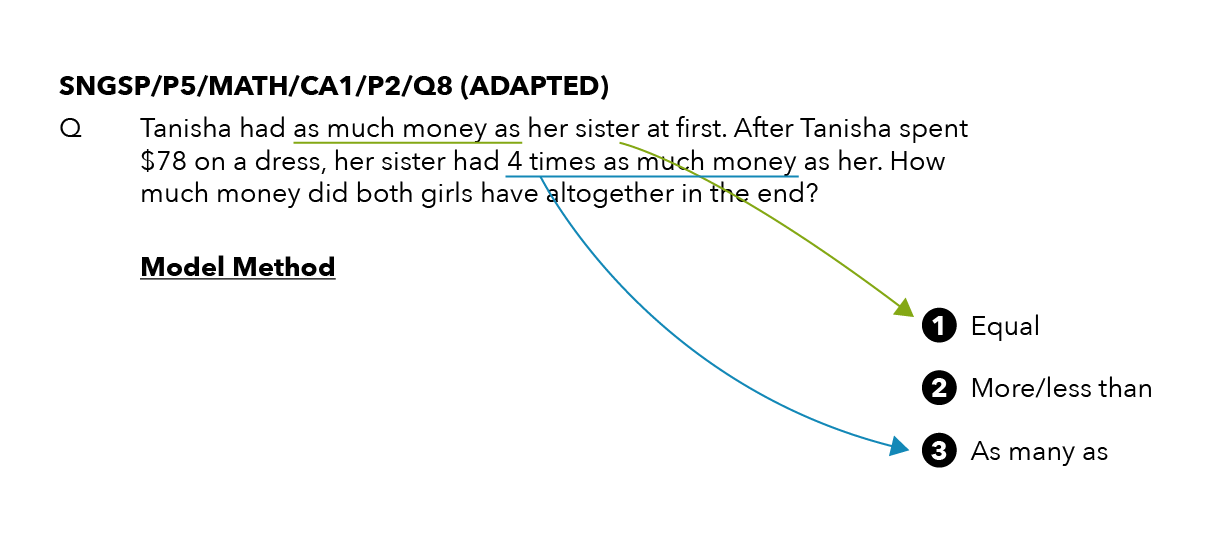
🔎 Equal
🔎 More/Less than
🔎 As many as
The most important keyword is equal, followed by more/less than, and then as many as.
Let’s go back to the question and label the key phrases:
Source: CHIJ St. Nicholas Girls’ School (Primary) – 2010 P5 CA1 Examination Paper
- “Tanisha had as much money as her sister at first” → Equal
- “Tanisha spent $78” → Change
- “Her sister had 4 times as much money as her” → As many as
Step 3: Draw The Models
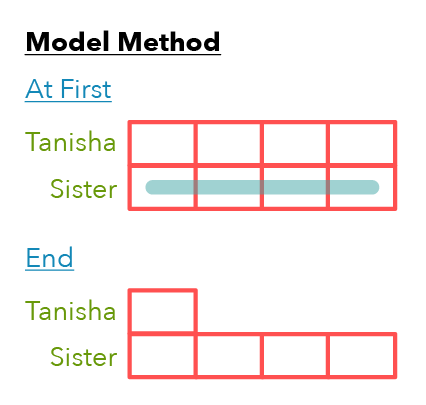
At first, Tanisha had as much money as her sister, meaning they each had the same amount. Let’s draw two identical bars to represent this equal amount.

Next, consider what has changed and what has stayed the same.
The second sentence describes the change: Tanisha spent $78, so she now has less money, while her sister’s amount remains unchanged.
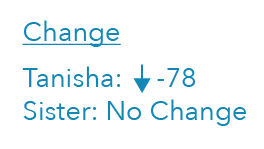
In the end, her sister had 4 times as much money as her.
If we convert “4 times” into a fraction, it will be 4/1.
The numerator of 4 goes to the first person (her sister) in the mentioned sentence, while the denominator of 1 goes to the second person (Tanisha).

At this point, some students would start drawing four boxes for Tanisha’s sister and one box for Tanisha.
But before we jump into drawing those boxes, we need to check what is kept the same.
💭 Why Do We Need To Check What Was Kept The Same? 💭
We will follow the size of the model that was kept the same as it helps us determine the size of the model to use.
So, between Tanisha and her sister, we will start with her sister first.
For our End model, let’s draw a bar the same size as the At First model to represent the sister’s amount of money, which stayed the same both at the beginning and at the end.
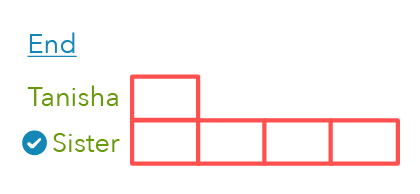
We know this bar represents 4 units, as identified earlier.
Let’s now divide the bar into 4 equal parts.

How many units does Tanisha have at the End? She has only 1 unit, so let’s draw one box to represent her End amount of money.
Step 4: Match Units and Find the Value
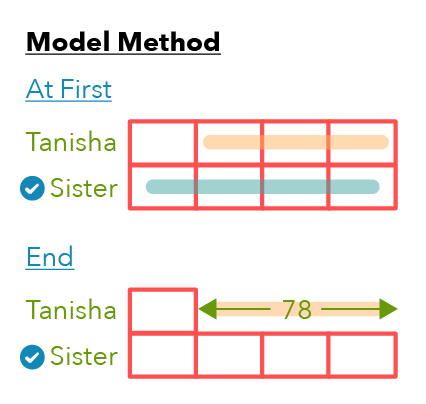
The next step is to make parts equal by cutting the At First model the same way we divided the End model.
Let’s split the At First model into 4 equal units for each girl.
Since Tanisha spent $78, and her amount decreased from 4 units to 1 unit, she must have spent 3 units.
We know these 3 units correspond to the $78 she spent, so the missing part in our End model represents this amount.
In other words, $78 is equal to the 3 units Tanisha had At First.
Therefore:
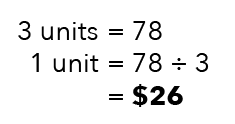
Step 5: Answer the Question
We’re asked for the total amount of money both girls had at the end.
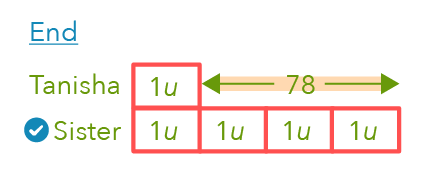
- Tanisha has 1 unit
- Her sister has 4 units
That’s a total of 5 units.
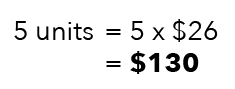
Final Answer
Both girls have $130 altogether in the end.
Conclusion
In this blog post, applying the One Item Unchanged strategy helped us break down and solve this tricky Whole Numbers word problem.
By drawing models, your child can visualise what remains the same in the question and make sense of how the other values change around it.
This is just one of the 4 Change Strategies that can be used for tackling such questions. As your child gets more familiar with each strategy, he/she will be able to pick the most suitable strategy for different scenarios. This helps them to become more confident and accurate problem solvers.
With practise, these strategies will make solving challenging word problems much more manageable for your child.




